基础机器学习算法：贝叶斯公式与朴素贝叶斯分类

数学与机器学习 概率,人工智能,机器学习,分类,朴素贝叶斯,贝叶斯公式,MINIST，手写数字 Comments

概率知识

条件概率

img

用韦恩图可以比较方便的理解条件概率。我们以掷骰子出现的点数为例，总的样本空间集合为S={1,2,3,4,5,6}，假设事件A为点数为偶数，那么A集合就是A={2,4,6}，B事件为点数大于3，B={4,5,6}。

很明显

现在假如我们已经知道了A事件发生了，也就是点数是偶数，这种情况下B发生的概率，就是条件概率，记作 $ P(B|A) $，也就是在A事件发生的前提下，B事件发生的概率。

既然A已经发生了，那么点数一定落在了A事件的样本空间中，这时候如果B发生，点数一定落在了AB的交集中，也就是AB发生了。

全概率公式

来看一个问题，假如一个人每天出行上班，坐公交车的概率是0.8，坐地铁的概率是0.1，开车的概率是0.1，而坐公交出车祸死亡的概率是0.0001，坐地铁出车祸死亡的概率为0.00001，开车出车祸死亡的概率是0.01，求这个人出车祸死亡的概率。

$ A_1 = 坐公交车 , A_2 = 坐地铁, A_3 = 开车 , B = 出车祸死亡 $

根据已知条件

我们要求的是：

B事件就等价于“{坐公交车并且出车祸死亡}或者{坐地铁并且出车祸死亡}或者{开车并且出车祸死亡}”，那

而根据前面的条件概率公式

所以我们要求的结果就是:

全概率公式：

设事件img是一个完备事件组，则对于任意一个事件C，有如下公式成立：

img

这个公式就是全概率公式，它的涵义就是一个事件可能由多个事件导致，最终的概率可由这些事件的概率计算得到。

贝叶斯公式

全概率公式的作用是“由因推果”，根据各种原因计算结果的概率，而贝叶斯公式，则是“由果推因”，比如上面的例子，已知这个人出车祸死亡了，求他开车的概率，也就是求

根据条件概率公式，

根据前面的计算结果，我们可以得到$P(A_3|B) = 0.9251$，也就是说，假如这个人出车祸死亡，那么它有92.51%的概率是开车的。

其实贝叶斯公式很简单。

我们再来举一个例子说明贝叶斯公式的应用。

假设女神喜欢你的概率为仅0.01，女生对喜欢的人笑的概率是0.99，而女生所有人笑的概率为0.9，现在已经知道，女神对你笑了，求女神喜欢你的概率。

假设 A = {女神喜欢你}，B={女神对人笑}，这两个概率已知，而且也知道女神对喜欢的人笑的概率,所以

用贝叶斯公式很容易求得

所以，虽然女神对你笑了，但是喜欢你的概率还是很低，虽然稍微提高了一点，为什么呢？因为女神对90%的人都笑，女神都这样。假如女神对大部分人都不笑，对你笑的话，那喜欢你的概率就很大了。

深入理解贝叶斯

我们先来看一个问题：

某种病的发病率为0.1%，也就是平均1000个人里有一个人的病，有一个指标，对于99%的患者，都呈阳性，但是也有5%的假阳性，就是没得病的人也有5%的人指标呈阳性。现在某个人指标呈阳性，那他患病的概率有多大？

凭直觉，我们会认为他患病的概率很大，我们来计算一下。

A = {患病}， B = {结果呈阳性} ，正常人和患者都有可能指标阳性，根据全概率公式

而

根据贝叶斯公式，

也就是说，这个人的病的概率不到2%，为什么会这样呢？因为这个病的发病率太低，而假阳性的概率又过高。

我们继续看这个贝叶斯公式。

其中的几个参数重新定义一下：

img

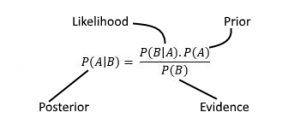
先验概率

我们把P(A)称为“先验概率“，即我们在不知道B事件的前提下，对A事件概率的主观判断。

可能性函数

公式里的P(B|A)/P(B)称为“可能性函数”，这是一个调整因子，即新信息B带来的调整，作用是使得先验概率更接近真实概率。

如果“可能性函数”P(B|A)/P(B)>1,意味着，“先验概率”被增强，事件A发生的可能性变大；
如果”可能性函数”=1，意味着B事件无助于判断事件A的可能性；
如果”可能性函数”<1，意味着”先验概率”被削弱，事件A的可能性变小。

什么情况下这个比值会增大呢？就是如果A发生导致B发生的可能性增大，那么就会导致比例增大，同样，如果A发生导致B发生的概率变小了，那比例也会变小。

以前边女神笑为例，女神如果喜欢一个人，那么她笑的概率从0.9升到了0.99，那么这个比例就成了1.1，所以如果女神对你笑，那喜欢你的概率也增大到1.1倍。

后验概率

P(A|B)称为”后验概率”，即在事件B发生之后，我们对A事件的概率的重新评估。

朴素贝叶斯分类

通过实例理解

贝叶斯分类是一种比较简单的机器学习分类方法，它依据的就是贝叶斯公式。我们把贝叶斯公式中的AB改一下：

我们要求的就是已知特征，它属于某个类别的概率是多少，概率最大的那个类别就是分类器输出的结果。

我们先看一个最简单的例子，假设我们统计了10000个适龄男性的特点（是否高富帅），然后随机找女生问愿不愿意嫁，得到了如下的数据。

是否高 是否富 是否帅 是否嫁
高 富 帅 嫁
高 富 不帅 嫁
不高 不富 帅 不嫁
不高 富 帅 嫁
不高 富 不帅 嫁
高 不富 不帅 不嫁
不高 不富 不帅 不嫁
不高 不富 帅 嫁
高 不富 帅 嫁

这只是一部分样本，一共有10000条数据，我们简化一下把1000条都表示出来。我们用X来表示高富帅三个属性，Y表示是否嫁。

经过我们整理，把数据整理成了下面的形式

X Y 样本数
000 0 4275
000 1 0
001 0 1300
001 1 125
010 0 25
010 1 200
011 0 2
011 1 73
100 0 2700
100 1 150
101 0 30
101 1 920
110 0 4
110 1 146
111 0 0
111 1 50

数据很现实，非高非富非帅的没有一个愿意嫁的，而高富帅没有一个不愿意嫁的。

有了这个表，我们就能得到一个分类器，输入为X,输出为y，y只有两个值，0和1。

什么意思呢？就是对于一个输入X，我们求出所有的P(Y|X)，然后哪个的概率最大，那么输出就是对应的Y。举个例子，我们要计算X=(1,0,1)对应的输出值，根据上表，我们很容易的可以得到

所以我们的分类器就能得到f(X=(1,0,1)) = 1，也就是高帅的人就可以嫁了。

看来贝叶斯分类很简单啊，只要列出一个表来就行了。我们继续来看，假设我们用分数来刻画高富帅的程度，分数是1-10分，那我们列的表行数就是10x10x10x2=2000行了，如果2000行还可以接受，那假如分数是1-100，有10个属性，那行数就是2*100^10，这个列表就不好列了吧。再假设，这个分数不是离散的，而是连续的，那就没法列表了。

我们暂时先不考虑连续的情况，先考虑离散的情况。我们需要做一个非常强的假设，就是这些属性是相互独立的，也就是

有了这个假设，我们就能把上面的例子中的2x2x2x2行数据改成三个表，每个表4行，也就是2x2x3行，

是否高 是否嫁 样本数
0 0 5602
0 1 398
1 0 2734
1 1 1266
“高”的数据
是否富 是否嫁 样本数
0 0 8305
0 1 1195
1 0 31
1 1 469
“富”的数据
是否帅 是否嫁 样本数
0 0 7004
0 1 496
1 0 1332
1 1 1168
“帅”的数据

这时候假如我们要求P(Y=1|X=(1,1,1))，我们没法直接根据样本数量进行计算，需要利用独立性做一些转换。

最后一个式子，我们都能从表中根据样本数算出来，最后的结果是P(嫁|高富帅) = 5！！为什么会出现概率大于1的情况呢？这是因为我们做了很强的假设，与实际效果不符，我们的P(嫁)用了整体的概率，但是其他的用了各自统计的概率。实际上

所以我们假设的两个相等的概率，实际差了5倍，我们最终得到的结果不是准的，但是这并不影响我们分类。因为

我们发现它们两个的分母是一样的，所以我们不必求出分母，只比较分子即可。

用了这种独立性假设后，假设每个属性是1-10分，我们只需要列3个表，每个表20行，一共60行，大大减小了问题的复杂度。所以我们把这种方法称为“朴素”贝叶斯(Naive Bayes)，就是天真的贝叶斯，把事情想得简单一点。

数学表示

假设我们得到了一个训练集

其中x是一个n维向量

里面的每一个值都是离散的，取值范围有限。

y的取值范围是就是分类的数量

假如我们能得到P(X,Y)的联合分布，那么我们就能得到任意的P(Y|X)。

img

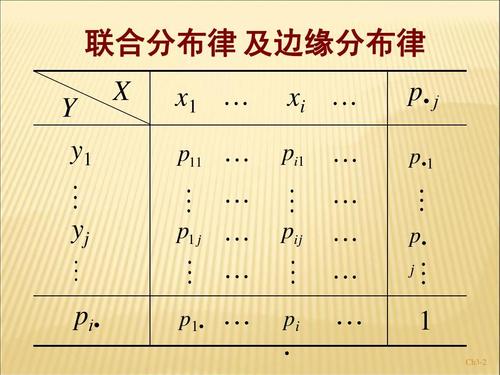
假设$x_i$的取值互相独立，那么

所以，分类器$f(x)$为

考虑到对于所有可能的取值，分母是一样的，所以

拉普拉斯平滑

我们在统计数据的时候，一些发生概率小的事件，很可能统计结果为0，这样就影响了我们对后验概率的计算，因为乘以0那结果必然为0了。

为了减少这种统计数量为0带来的影响，我们把每个可能的取值发生的频数加上一个固定值$\lambda$，这样

其中k是$X^j$的取值范围数量。当$\lambda=1$时，我们就称为拉普拉斯平滑。

实战：用朴素贝叶斯识别手写数字

先把MINIST手写数字集下载下来，地址是https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz ,

我们可以用下面代码展示一下：

1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
import numpy as np

data = np.load('mnist.npz') #具体的路径
x_train, y_train, x_test, y_test = data['x_train'], data['y_train'], data['x_test'], data['y_test']
print(x_train.shape)
print(y_train.shape)
plt.imshow(x_train[0])
plt.imshow(x_train[1])
plt.show()

我们可以看到，能从里面拿到4个数据集x_train, y_train, x_test, y_test，前面的是训练集，后面的是测试集。

x_train的shape是(60000,28,28)，也就是60000条数据，每条数据是一个28x28的矩阵，也就是一个图片，每一个矩阵点的大小是0-255，代表一个像素。y_train是60000个标签，代表每个图是什么数字。我们用plt可以画出来。

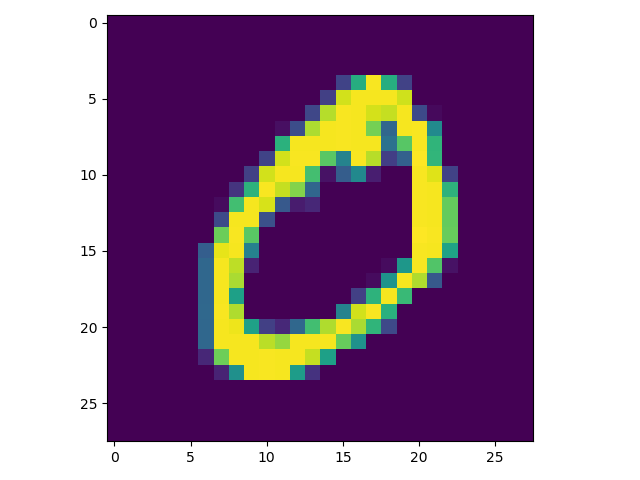
image-20200513170938962

下面是用来识别的完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import numpy as np
data = np.load('mnist.npz')
x_train, y_train, x_test, y_test = data['x_train'], data['y_train'], data['x_test'], data['y_test']

#把(60000,28,28)展开成(60000,784)，这样每个样例都是一维的，便于处理
x_train = x_train.reshape(x_train.shape[0],28*28,order="C")
x_test = x_test.reshape(x_test.shape[0],28*28,order="C")
print(x_train.shape)

#training

#对于每一个数字，都有一个矩阵,代表每个像素点每个像素值出现的次数
# 为了计算P(Xi = xi | Y=c),比如P(X0=0|Y=0)=0.99, P(X0=255|Y=0)=0.0001, P(X1=0|Y=0)=0.001，这是一个联合分布律
# 先把次数统计出来，后面计算概率
'''
数字0对应的矩阵
      0    1    2    3    4    5    6    7    8    ...    255
x0    100  3    0    0    0    0    0    0    0           0 
x1    90   5    3    1    0    1    0    0    0           0
x2
x3
...
x784
数字1对应的矩阵
'''
# 所以该矩阵的shape是(10,784,256)，为了保证每个像素值出现的次数不为0，以1初始化
distribution = np.ones(10*784*256).reshape(10,784,256) #拉普拉斯平滑，认为每个值都至少出现了一次

# 统计每个数字出现的次数，以便计算P(Y=C)
digit_count = np.zeros(10)

for i in range(x_train.shape[0]):
    digit_count[y_train[i]] = digit_count[y_train[i]] + 1 # 相应的数字个数加1
    one_hot = np.eye(256)[x_train[i]] # 把这个训练数据(784,)，做one_hot编码，可以直接累加频数
    distribution[y_train[i]] = distribution[y_train[i]] + one_hot


#计算条件概率,也就是把distribution从频数变为概率
for i in range(10):
    distribution[i] = distribution[i] / digit_count[i]
print(digit_count)

#计算P(Y=c)
digit_prob = digit_count / 60000

#predict,拿100个测试样子试试
errorcount = 0
for i in range(100):
    x = x_test[i]
    one_hot = np.eye(256)[x]
    ret = distribution*one_hot #这个地方有点不好理解，其实就是one hot了之后相乘，那么只能取到对应像素值的概率，其他位置都是0，相当于计算了所有P(Xi=xi|Y=c)的值
    ret = ret.sum(axis=2) #每一行只有一个正值，其他是0，相加，减小维度，下面再相乘

    p = np.ones(10)
    for j in range(10):
        for pp in ret[j]:
            p[j] = p[j]*pp #按公式里的进行累乘，因为x有784个feature，所以要乘784次


    p = p * digit_prob
    print(p)   # 这个就是x对应的取y的概率
    y = np.argmax(p) #找到最大的下标即可
    print("predict:",y,",real:",y_test[i])
    if y != y_test[i]:
        errorcount += 1
print(errorcount)

但是结果让人很失望，因为100个中错了66个，而且大部分都被预测成了0，我们看一下概率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
[0.00000000e+000 9.77321365e-200 3.69171333e-259 4.08106118e-265
 7.02894044e-274 5.64538703e-262 2.01724366e-279 2.77597583e-273
 2.21950679e-254 1.14471578e-272]
predict: 1 ,real: 1
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
predict: 0 ,real: 3
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
predict: 0 ,real: 6
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
predict: 0 ,real: 9
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
predict: 0 ,real: 3
[0.00000000e+000 4.73491927e-255 3.20480193e-309 1.78647460e-315
 0.00000000e+000 3.72016980e-310 3.26325578e-311 0.00000000e+000
 7.87593251e-310 0.00000000e+000]
predict: 1 ,real: 1
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
predict: 0 ,real: 4

为什么会预测成0呢？因为概率相乘后，已经小到Python没法识别的精度了，基本上都是0，那肯定选第一个。之所以相乘后接近0，是因为有784个feature，784个小于1的数相乘，基本上很难不是0了，所以我们做下优化，我们在每次相乘的时候给乘一个大于1的数，这样结果不会太小。但是这个数也不能太大，否则又成了天文数字，这样的数就是我们需要手动调整的参数。我们在下面这行乘2试试

1
p[j] = p[j]*pp*2

现在100个只有15个识别错误，但是看概率乘积，还是比较小，再增大一点到3，14个错误，已经可以了。我们预测1000个，错188个，识别率超过80%，算是一种合格的算法。

ifool金融IT民工

Java工程师，对机器学习、云计算、安全都感兴趣